Our Technology
Our Technology
SPAIDER trains neural networks to speed-up numerical simulations and to enable real-time performance predictions.
Our technology can be applied to several fields of physics, such as:
CFD | FEM | CEM
Designers can make informed decisions and improve their design. On the spot.

Fundamental Technologies
In the field of Optimization, several methods are available to improve the performance of a design or to speed-up the design process itself.
The SPAIDER team has great experience in mathematical models and optimisation techniques. We evaluate the best approach to adopt on a case-by-case basis in order to achieve maximum productivity.
Local methods
Global research methods
Convolutional neural networks
Graph neural networks
Surrogate models
Local Methods
In numerical and experimental data analyses, gradient-based optimization methods, such as gradient descent, are widely used for finding the minimum value of a function. By calculating the derivative (i.e. gradient) of the function, these methods iteratively update model parameters in the direction of the steepest decrease. This makes them efficient for continuous, differentiable problems. For numerical simulations, gradient methods can optimize model parameters to better match experimental data, while in experimental settings, they fine-tune models to improve prediction accuracy with fewer evaluations of the system.
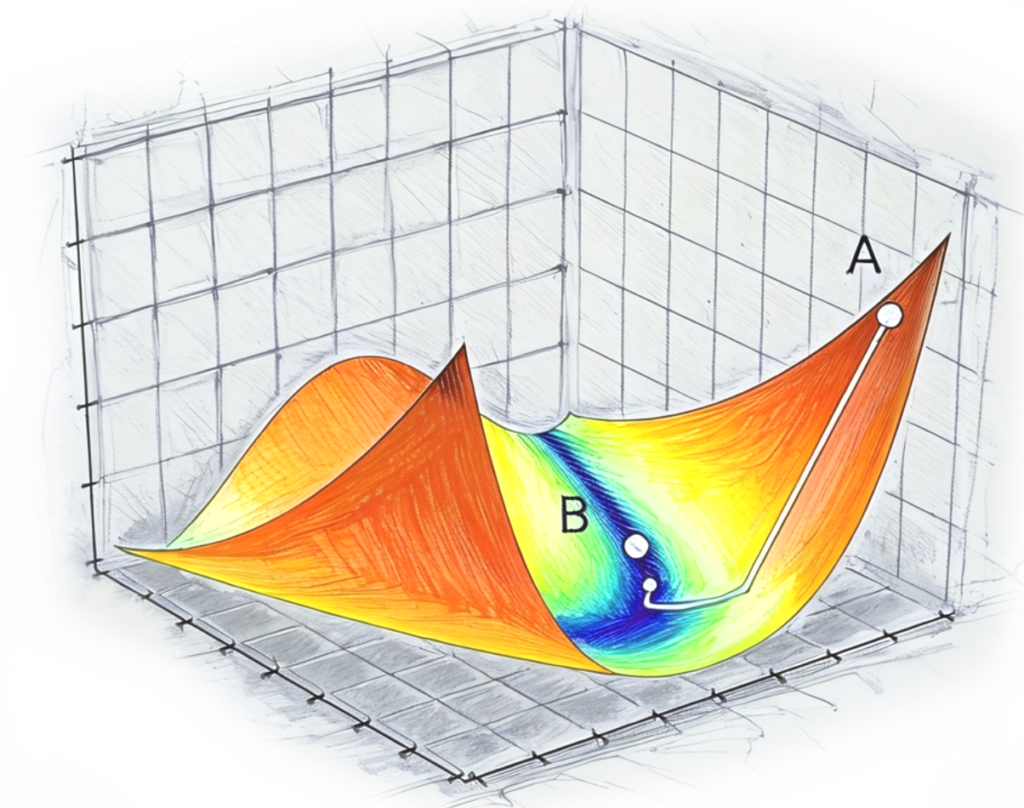
Global Research Methods
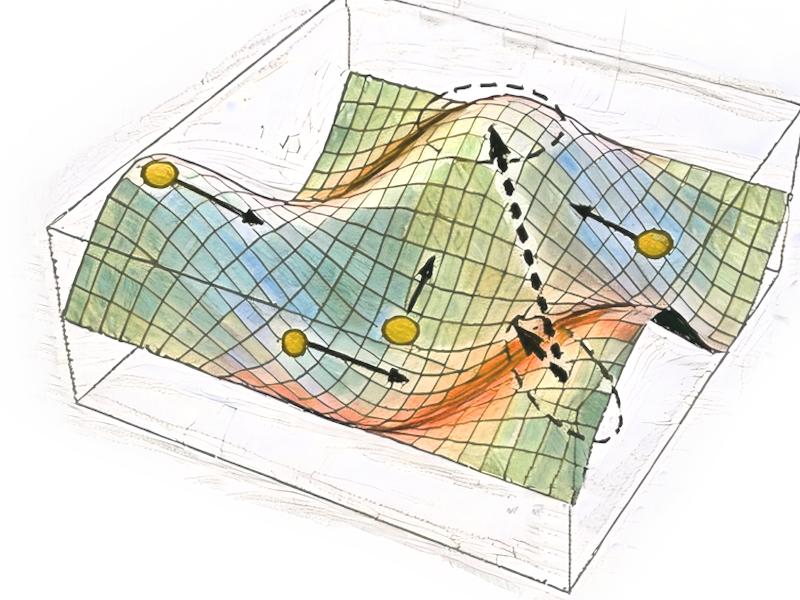
Global research methods, including genetic algorithms, simulated annealing and particle swarm, are well suited to explore the entire solution space, making them ideal for problems with complex, non-convex landscapes. Unlike local methods, these techniques do not rely on gradient information and instead explore a wide range of solutions to avoid being trapped in local minima. In numerical analysis, global methods can help identify optimal solutions for highly non-linear models, while in experimental data analysis, they enable the discovery of the best-fitting parameters by searching through diverse configurations, particularly when experimental data is noisy or uncertain.
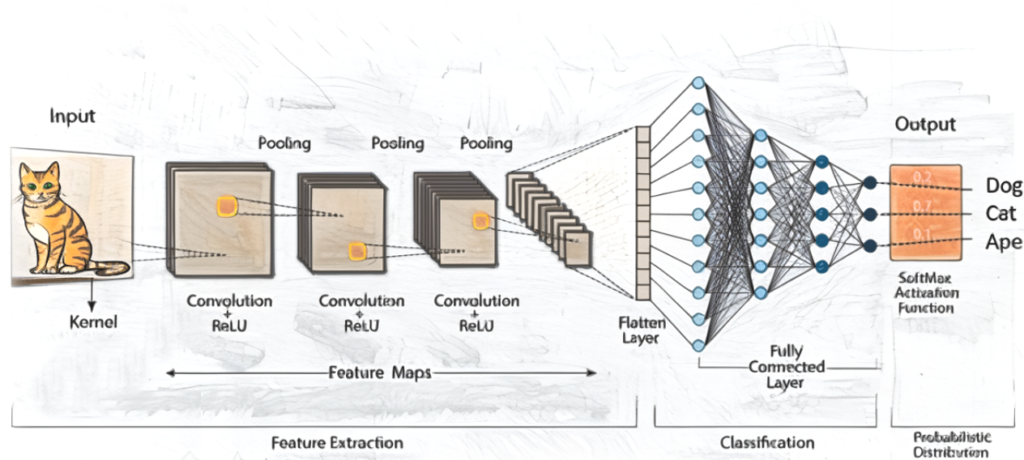
Convolutional Neural Networks (CNNs)
Convolutional Neural Networks (CNNs) are particularly effective in handling data with spatial structures, such as images or time-series data. In numerical analysis, CNNs are used to optimize feature extraction by learning spatial hierarchies within the data, improving model performance in tasks like image recognition or signal processing. In experimental data analysis, CNNs can process complex experimental results, such as sensor readings or microscope images, to automate feature identification, speeding up analysis and optimizing model predictions, especially in high-dimensional datasets.
Graph Neural Networks (GNNs)
Graph Neural Networks (GNNs) are optimized to work with data represented as graphs, where nodes represent entities and edges represent relationships. In numerical analyses, GNNs are applied to problems involving structured data like social networks, chemical compounds, or transportation systems, where relationships between data points are as important as the data itself. In experimental data analysis, GNNs help optimize the prediction of outcomes where relational data plays a key role, such as in the analysis of material properties or biological networks, enabling a deeper understanding of complex systems by capturing interactions that traditional models might miss.

surrogate models
Surrogate models are widely used in engineering numerical analyses to approximate complex, computationally expensive simulations with faster, more efficient mathematical models. These models, also known as metamodels, enable engineers to perform optimization, sensitivity analysis, and uncertainty quantification without repeatedly running costly finite element or computational fluid dynamics simulations. Techniques such as polynomial regression, Kriging, radial basis functions, and neural networks are commonly employed to construct surrogates that accurately capture the input-output relationships of engineering systems. By leveraging surrogate models, engineers can significantly reduce computational costs while maintaining reliable predictions for design and decision-making processes.

